Codeforces Round #345 (Div. 2) Problem B

题意

给一个整数序列，长度小于1000，每个元素元素小于1000大于1，把这个序列任意排序，使得相邻的两个数字满足$a[$i] < $a[$i+1]的pair的个数最大。只需要输出最大的pair个数。

其实画图可以很形象地说明问题。这些图都是用Emacs画的，挺有意思。

首先统计出每个数字的个数。接下来：

第一种思考角度如下图：

从小到大比较相邻组的大小，把较小的那一组的大小累加起来，然而要不要累加较大的这一组的大小那就要看是不是有别的组的大小比它还要大。从下面的图的第2列和地5列可以看到这样的情况。因此还要记录一个最大值。

这个角度从图里面看是从左往右。a -> b -> c -> d这样的顺序。

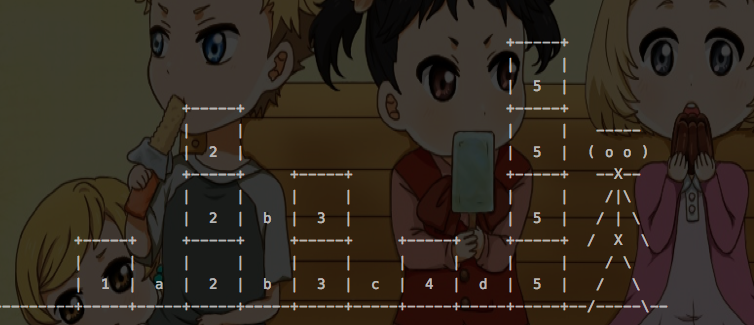
第二种思考方式如下图：

第一种是从左往右，那么就可以从下往上。其实这样也是合理的。每次从一组里面取出最下面的一个，累加起来。a -> b的顺序。

不过这个方法实现的时候需要一点技巧。

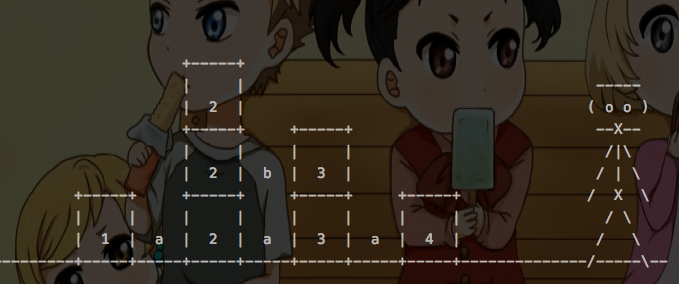
然而，最简单的做法还是这样：）

$\ = $/;
while (<>) {
    $n = $_; $h->{$_}++ for split ' ', <>;
    print $n - (sort {$b <=> $a} values %{$h})[0];
}

其实画图有局限性，从另一个角度想，把数列分成尽可能长的严格递增（或者只含有一个元素）的子序列，那么每一组一定会含有在整个序列中出现次数最多的那个数字X，如果某个子序列不含有数字X，那么它不足够长。如果某个子序列含有两个数字X，那么它不是严格递增。设整个序列长度为N，在序列中出现次数最多的数字X出现的次数为P，那么就可以分成P个子序列。整个序列中，相邻两个数字递增的pair最多为N-1，分成P个子序列之后，相邻两个数字递增的pair减少了P-1个，所以答案就是 (N - 1) - (P - 1) = N - P，也就是整个序列的长度减去出现次数最多的数字出现的次数……